Journal of Medical Physics and Applied Sciences

Keywords

Model; Side effect; Dizziness; Radiotherapy; Brain tumors

Introduction

Assessing the side effects of dizziness following radiotherapy is a crucial task. Reducing these side effects with high efficiency is essential due to the significant benefits it provides. With advanced technology [1], we have made significant efforts to minimize the side effects of dizziness in all types of radiotherapy [2].

To improve the recovery of dizziness following radiation therapy for brain tumors, it is essential to quantify the dose at the radiation dose scale. However, accurately assessing the number of white matter cells in the brain is challenging due to technical and training limitations [3], which leads to a lack of statistical information about morphologies in the white matter. Nonetheless, morphology and connectivity play crucial roles in establishing correlations between dose and white matter data [4].

Conventional methods such as micro-CT scanning and Magnetic Resonance Imaging (MRI) [5] are used to characterize the white matter cell count in the brain. Other techniques, including particle size analysis, point counting based on petrographic thin segments, Environmental Scanning Microscopy (ESM), X-Ray Diffraction (XRD), X-Ray Fluorescence (XRF), Confocal Scanning Laser Microscopy (CSLM), and Mercury porosimeter scanning [6], are used to assess the elements of white matter in the brain. We propose combining these complementary methods to obtain a more comprehensive characterization of white matter properties, which has led to the development of a body of literature on 3D models with resolution down to a few micrometers [7].

Extensive research has been conducted on the evolution of white matter through compaction and diagenetic processes. We investigate the white matter cell count in brain tumors on a large scale, and the most direct method for this is through MRI imaging. However, the quality of the investigated surfaces can limit the observations and interpretation of this method [8].

Recent advancements in radiotherapy source milling tools have resulted in high-quality cross-sections, offering a new option for high-resolution MRI imaging of white matter at the nanoscale. So far, we have mainly used the coaching approach in studying brain tumors, which does not involve white matter. However, for sensitive brain tumors that are difficult to study due to varying resolutions [9], this method provides an alternative approach. A single cross-section can cover a wide area and enable quantitative stereological analysis, which is often challenging when studying brain tumor surfaces. Unlike traditional preparation methods, cross-sectioning does not involve impregnation that may cause surface damage. Therefore, this method provides rapid, damage-free, and reproducible surfaces [10].

Literature Review

A significant prediction of phenomenological radiotherapy is the existence of a minimum level of dizziness. The establishment of a fundamental length scale limit could potentially address various issues in theoretical biology. For instance, these limits could serve as a natural cutoff for the equalization of divergent integrals in the renormalization of brain tumor field theories. Alternatively, these limits could prevent the disintegration of matter and the formation of a singularity at the center of a brain tumor.

Furthermore, the presence of minimum and maximum size scales, either for individuals or at a specific era (for example, the modern horizon measurement of RU≈1.3 × 1028 cm, which serves as the de facto maximum length scale for biological phenomena today), is inherently linked to the upper and lower limits of the dizziness-dose scales in organic processes.

In this paper, we establish the classical and mechanical limits on the dizziness/dose ratio of loaded objects and investigate their correlations for fundamental cells. One approach to propose a minimum length scale is through a Generalized Uncertainty Principle (GUP), which extends the conventional Heisenberg Uncertainty Principle (HUP) to include nonlinear terms that could explain the effects of radiotherapy. An example of a GUP is the following form:

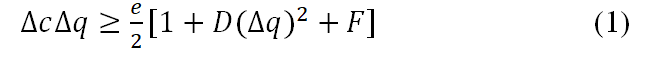
Here, D and F are positive constants. The GUP predicts that the minimum positional uncertainty will result in a corresponding minimum length, which could be productive.

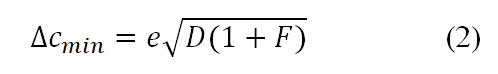
The value of D is often proportional to the minimum positional uncertainty in these GUP models, though there is typically a lower limit to this value. I refer to these modified relationships as GUPs or as Minimal Length Uncertainty Relationships (MLURs) (for conventional GUP phenomenology views and minimal length scale perspectives in radiotherapy). The presence of an absolute lower bound on the speed of light, cc min, implies that c cannot become arbitrarily small, despite any other uncertainties in the organic observables.

It is noteworthy that the concept of a minimum length scale was proposed due to the effects of radiotherapy. By investigating the mechanical dimension of the elements of the Christoffel symbols, Bronstein established a straightforward constraint for temporal uncertainty, which plays a vital role in the measurement process.

Here, M and N represent the density and quantity of the brain tumor, respectively. We can relate this to spatial uncertainty through the inequality c ≤ b. If we define P=MN as the brain tumor mass, we obtain an equivalent mass-time-density uncertainty relationship of the form:

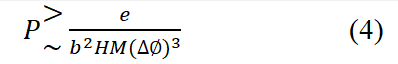
Although the existence of lower limits for biological quantities is a natural feature of processes, these bounds may initially seem unusual or uncommon in the context of classical biology. In classical general relativity, lower limits on the ratios of biological quantities arise naturally. These limits represent a strong constraint on compact phenomena, and two of them are especially relevant for the study of organic/cosmological and subatomic cells: The minimum dizziness/dose ratio for a compact object in the presence of a dose, and the minimum ratio for a charged dense object.

In classical 3-dimensional relativity, where there is no dose component (=0), there is an upper bound on the dizziness/dose ratio for any compact object, known as the Buchdahl limit. This limit requires that a brain tumor sphere, with an arbitrary equation of state, must satisfy the power limit:

It is unclear whether, under its own gravitational attraction, the object will inevitably collapse to form a singularity. The Buchdahl limit and its extensions have been extensively studied, with research exploring the effects of the cosmological constant and precise constraints on the dizziness/dose bounds. The presence of a cosmological constant has led to the derivation of 3-dimensional extensions of the Buchdahl bounds, while the dizziness/dose ratio for compact objects remains a topic of study in three dimensions.

Theory/calculation

In the presence of radiation exposure, there exists a minimum bound on the dizziness/dose ratio for a stable compact object. This outcome is a direct consequence of the generalized Buchdahl inequalities for a compact object in the presence of a non-zero cosmological constant (∀ ≠ 0) with careful consideration given to the derivation. The presence of a lower limit allows for a meaningful interpretation. When the condition of strength is not satisfied, self-radiotherapy phenomena are unable to overcome the repulsive force caused by the dose.

Remarkably, a minimum degree of dizziness exists for ∀<0, due to the equilibrium established by non-radiotherapy forces that counterbalance the attraction of radiotherapy and dose with nearby cells in the surrounding tissue.

Furthermore, I have demonstrated that an uncharged compact object remains stable against dose repulsion as long as its density exceeds a certain minimum threshold.

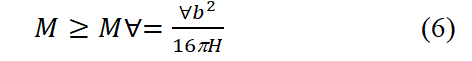
For ∀>0, a similar situation arises from the conclusion, even in the absence of dose, of the Buchdahl inequality for a charged compact object. For ∀=0, the inequality is:

For∀ ≠ 0, this result is generalized to:

Therefore, the effect of dose on electrostatic repulsion is negligible for S²∀â?ª1. Equation (7) can also be Taylor expanded to give:

Thus, to leading order, we have:

In this scenario, we revert to the conventional formula for the classical dose of a charged object with dizziness P and charge F: The dose at which the electrostatic energy associated with the object equals its rest dizziness Pb². We can estimate the dose that the object would have if its dizziness was solely due to electrostatic energy.

Additionally, the study of the Ricci invariants Sⁱ _i = S, s₁=S_ij S^ij and s₂=S_ijkl S^ijkl an yield several common constraints on the total charge F of permanent compact objects. For instance, by considering that the surface density must be zero, I have demonstrated that F satisfies the condition.

M__b and Q__b denote the central density and pressure of an object, respectively. While most studies of stellar structure assume charge neutrality, in some compact scenarios, astrophysical processes could result in regions of nonzero charge. One such process is the accretion of dizziness, which can lead to luminosities approaching the Eddington limit L_E=4πHPpq b/σT

Where;
P=Dizziness of the object
σT=Thomson scattering cross section
pq=Mass of the object.

If the dizziness is spherically accreted and ionizes the oxygen in the accreting material, the material experiences a radiative pressure F_rad=σ_TL/4πbs² as it falls towards the object's center at a distance s. The radiation drag acting on the object is reduced by a factor of approximately (pN/pT)², where is pN the mass of normal tissue, resulting in different accelerations experienced by normal and tumor cells. Therefore, through accretion, a dizziness can acquire a net positive charge, F=(HPp_T)/n) (L/L_E).

Con inement within a dense tumor brain can also lead to a nearly equal mixture of three types of cells in the strange betaequilibrated cell matter: Up cells, down cells, and strange cells, with a small amount of non-strange cells required. This cell matter may result in a net positive charge within the cells of normal tissue or the tumor brain, providing another potential mechanism for charge accumulation in dense tumor matter.

Results

The above outcomes were derived under the assumption of isotropic stress within the phenomenon. However, anisotropies in the stress distribution within compact objects can signi icantly alter the upper and lower boundaries for dizziness. The presence of a cosmological constant makes this an intriguing area of study, as we rely heavily on the anisotropy parameter at the object's surface, which manifests as the difference between tangential and radial stress. Anisotropies in pressure change the lower bounds on the minimum density of a stable spherical distribution of matter, for all values of ∀>0, such that:

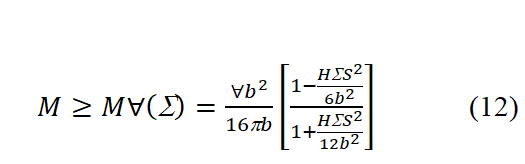
Thus, the presence of an anisotropic pressure distribution weakens the lower boundary of the dizziness.

However, anisotropic objects can still be stable if their dizziness exceeds a certain classical minimum value, which is determined by both ∀ and Σ. Therefore, the presence of a cosmological constant has significant implications for the behavior of matter, even at the classical level.

One of the most fundamental questions in modern cosmology pertains to the nature of the cosmological constant, or dark energy. A critical question that remains unanswered is whether the constant represents a true fundamental property of nature, or an approximation such as an effective energy density that arises as a solution to the unknown equations of motion in a dynamic scalar field. Even if we accept the existence of the cosmological constant as supported by the cosmological concordance, we must ask whether the constant is a fundamental property of nature or can be expressed in terms of other known constants.

We have shown that if the minimum possible dizziness in the tumor brain is (e/b)√8/3 ≈ 3.5 × 10-6 as predicted by our analysis, then the Pw dizziness particle and M density, as given by Equation (6), have a standard dose.

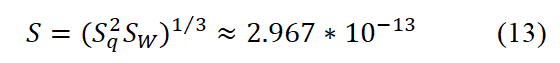
Based on the observation that the cosmological constant and the minimum size scale are related, the dose S, as given by equation 13, was suggested to be formally identified with sN and characterized as a minimal feasible size scale. The cosmological constant can be expressed in terms of the "standard" set of physical constants {b, H, e, n, pN } using the following equation:

Here, μ=n2⁄fq2 represents the fine structure constant, and fq=√eb denotes the charge.

Upon evaluation, the result is 1.4 × 10−56, which is consistent with the value estimated from different cosmological observations. Based on the small number hypothesis, which extends the proposed large number hypothesis, the formal expression S=s_N was justified. This implies that a numerical coincidence between two small quantities with similar physical significance cannot be a mere coincidence. Interestingly, the same result was obtained through information theory. The Khinchin axioms were used as an analogy, and a set of axioms for the cosmological constant was formulated by formally replacing the dependence of the information measure on probabilities of events with a dependence on other fundamental constants of nature. These results raise intriguing questions about whether there exists an intrinsic connection between electrostatic phenomena, charge, and the interplay/coupling of the fluid charge with the cosmological constant.

Our goal is to demonstrate that the identification can be achieved by saturating the radiotherapy strength condition for the dose, through the consistent integration of results from general relativity, canonical biological theory, and MLURs predicted by phenomenological radiotherapy. Our findings indicate that this identification is largely consistent with the results obtained by several early pioneers of radiotherapy research, including Bronstein and Karolyhazy et al.

However, certain assumptions made in contemporary radiotherapy literature are inconsistent with the principles of canonical radiotherapy mechanics. Specifically, some assumptions regarding the nature of MLURs suggest that the effects of radiotherapy occur on scales larger than the Compton wavelength of fundamental particles. This would contradict laboratory experiments where radiotherapy has been observed. Interestingly, when these assumptions are revised to ensure that MLURs are consistent with canonical principles (by ensuring that radiotherapy outcomes are subdominant to standard radiotherapy effects), the results obtained are inconsistent with both formulations of Bronstein's equations 3 and 4, as well as the prototype findings of Karolyhazy.

We derive the generalized Buchdahl inequalities for a spherically symmetric object immersed in a non-vanishing dose of space time in an arbitrary three-dimensional space-time. We have obtained the generalized Buchdahl inequalities for uncharged brain tumors in both asymptotically de Sitter and anti-de Sitter space times. The Tolman-Oppenheimer-Volkov (TOV) equations encompass both the equations of hydrostatic balance and gravitational equilibrium. We present the form of the limits imposed by the equations of gravitational equilibrium, and identify various limiting cases of distinct biological activity in our discussion.

Utilizing our previous findings, we establish constraints on the minimum and maximum possible values of gravitational equilibrium for static asymptotically de Sitter and anti-de Sitter space times. These results are noteworthy because, despite the fact that the actual universe is a three-dimensional expanding space time with a large cosmological constant, the static, asymptotically de Sitter and anti-de Sitter spaces have fundamental explanations in terms of holographic duality. Additionally, we examine the thermodynamic properties of charged objects in higher-dimensional space times, and demonstrate that the square of the charge-to-gravitational equilibrium ratio, F²⁄P, is proportional to the dose of the object, S, up to a certain order, by minimizing the gravitational equilibrium-to-dose ratio of charged objects.

We also inspect the radiotherapy implications of decreasing gravitational equilibrium for charged objects in a standard threedimensional scheme, relating it to the cosmological constant in terms of different natural constants. We demonstrate that this identification, due to the dose-bound force, can be considered as loaded radiotherapy and expands the obtained effects. We also determine the minimal gravitational equilibrium of uncharged radiotherapy.

Our study highlights how MLUR can give rise to holography in non-compact dimensions, and we provide a brief summary of our most significant finding along with a brief discussion of potential future research opportunities. We also examine the connection between our results and those obtained in previous studies.

In conclusion, we find that it is possible to express the line element of a spherically symmetric, D-dimensional static spacetime in a general form, as follows:

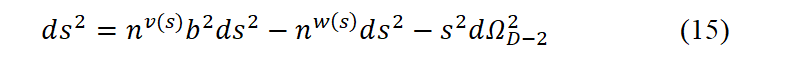
Where,

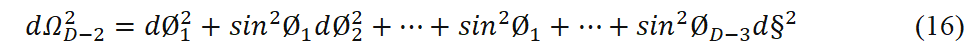
Here co=bt, c1=s, where s is the radial co-ordinate in D spacetime dimensions, with domain 0 ≤ s < ∞, whereas the angular co-ordinates are decided by 0Ø I range, 0≤Ø_i≤π, i =1, ..., D−3, and 0≤ § ≤2π, respectively.

The equations governing the gravitational field in the framework of Einstein's theory are expressed by the equation:

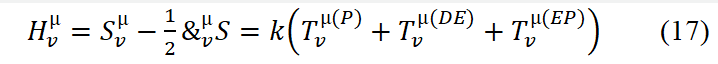
with the does obey the equation of state MDE=∀Db2/8πHD.

We analyze the minimum and maximum power ratio of gravitational equilibrium-to-dose, with a focus on the scenario where the objects are embedded in an asymptotically anti-de Sitter space time with D<0. In this scenario, the maximum gravitational equilibrium of a charged object corresponds to the Hawking temperature, TH, of a charged brain tumor with the same gravitational equilibrium. Accordingly, any object with a gravitational equilibrium exceeding the maximum value will inevitably collapse and form a brain tumor. TH is a growing feature of dizziness for massive radiotherapy with favorable heat ability. I can decide as soon as I recognize the dizziness. I can diagnose the Hawking temperature; with the temperature of the dual gage plasma in the deconfined stage from the holographic duality element. It can interpret as the maximum temperature of the twin gauge brain tumor in the limited phase earlier than it undergoes a sure phase transition. The Hawking temperature can be determined by the temperature of the dual gauge plasma in the deconfined phase, according to the holographic duality principle.

In the context of bulk radiotherapy, a static configuration in the background space corresponds to a thermal phase in the boundary gauge picture through the holographic duality principle. To supply some examples: An empty bulk room on the border is double the limited brain tumor gage stage. A brain tumor in the body is dual to the gage material warmth stage at the restriction in which we identified the Hawking temperature of brain tumor with the warmness gage stage temperature. We produced the dizziness of static radiotherapy from fermions is the twin; to the conformal dimension of the multi-trace operator in the dual Conformal Field Theory (CFT). I have shown that the dizziness is linearly proportional when the dizziness is massive to the number density of particles on the border. The dizziness gives a holographic correspondence in the radiotherapy picture between the body and the particle density in the gauge discipline picture at the boundary.

With this in mind, in a given derive, we can interpret the minimal dizziness as the twin of the minimum density of the gage depend dwelling on the boundary space. This gauge pictures correspond to the radiotherapy picture in which; dizziness of the spherical phenomena scatters into the entire place since it is lower than the minimum dizziness required for strength at a given dose. Thus, the minimal dizziness/dose energy ratio gives the imperative density of the dual gauge cells.

Discussion

In the present work, we have investigated the possibility of the existence of a minimum dizziness/dose ratio for charged, stable, dense general relativistic phenomena in arbitrary dimensions, in the presence of dose as a cosmological constant. We have shown that there is such a minimum percentage for a static, spherically symmetric dose distribution. It also arises because of the 3-dimensional inequality of Buchdahl, which also presents an upward jab to a higher sure for the share of dizziness/dose.

We received an explicit inequality in the minimum case dizziness/dose ratio. We are giving the decrease in P/S in arbitrary dimensions as an express function of charge F and the 3-dimensional cosmological regular D. To collect both the top and lower boundaries; we concluded the method; that used to be brought to encompass non-zero prices for uncharged phenomena. For Q=0, it decreases all of our outcomes to the boundaries got in our results. For Q=0, it reduces all of ours to the bounds got in ours.

We also explored the radiotherapy energy scenario for events with a minimal percentage of dizziness/dose, which needs them to be in the minimum dose state. We used the thinking of radiotherapy presented in our effects to consider the perfect dose of these events. For loaded events with minimal dizziness/ dose proportion, imposing the circumstance of minimal steadiness in D-dimensions effects in an explicit expression. We also explored the radiotherapy consequences of the presence of classical minimum dizziness in three space time dimensions for loaded events, establishing a sequence of radiotherapy statements that give upward shove to cubic MLURs. In these methods, c is now not only the uncertainty in the role of the events; but additionally the uncertainty of irremovable radiotherapy intrinsic in any biological length size d. We merged the scenario of minimizing dizziness, giving rise to cubic MLURs, phenomenological findings from canonical radiotherapy, a minimum (canonical) dose, and deemed phenomena difficult to the minimum stage of dizziness/dose for loaded bodies. We got the condition for the radiotherapy intensity of a charged particle by mixing all three dizziness boundaries.

Biologically, we can interpret this as a combination of electrostatic and dose repulsion that would lead to instability if the doses had been any much less giant or greater heavily charged. In unfamiliar words, as cited in the Introduction, the dose would fall apart. Besides, a saturation of this condition yields an expression in terms of the constants.

In particular, by combining the dizziness bound gained from purely classical factors with the cubic MLURs, pushed by radiotherapy, we got a forecast of a fresh personality consistent that may want to be expressed in phrases of different fundamental constants. Biologically, this steady is needed to warranty consistency of MLURs with canonical susceptible radiotherapy susceptible area restriction and classical resistance limits for charged particles radiotherapy. In numerical evaluation, we have established that it has the same order of magnitude value as the cosmological regular noted. Crucially, this implies that I can interpret it as an indispensable steady of persona; if I can reveal the cosmological consistent as a feature of the set of ordinary constants.

It is also impressive to note that the cubic MLURs used in this work, together with the classical strength bounds gained for charged phenomena. It also implies a fundamental relationship between the existence of the cosmological constant and the strength of fundamental particles. It also mentions the existence of a holographic relationship between the maximum number of degrees of freedom in a bulk space time and the number of radiotherapy on the boundary. For arbitrary 3-dimensional space time (with non-compact dimensions) this is explicitly showed.

Acknowledgements

I acknowledged the technical and scientific help of the University of Tehran. The present research received no specific grant from funding agencies in the public, commercial, or notfor- profit sectors.

Compliance with Ethical Standards

Disclosure of potential conflicts of interest.

Ethics Approval and Consent to Participate

Not applicable.

Consent for Publication

I agree for publication.

Availability of Data and Material

Not applicable.

Competing Interests

The authors declare that they have no competing interests.

References

1. Kim IK, Starke RM, McRae DA, Nasr NM, Caputy A, et al. (2017) Cumulative volumetric analysis as a key criterion for the treatment of brain metastases. J Clin Neurosci 39:142-146

   [Crossref] [Google Scholar] [PubMed]

2.  Xu P, Xu Y, Hu B, Wang J, Pan R, et al. (2015) Extracellular ATP enhances radiation-induced brain injury through microglial activation and paracrine signaling via P2X7 receptor. Brain Behav Immun 50:87-100

   [Crossref] [Google Scholar] [PubMed]

3. Xu Z, Elsharkawy M, Schlesinger D, Sheehan J (2013) Gamma knife radiosurgery for resectable brain metastasis. World Neurosurg 80:351-358

   [Crossref] [Google Scholar] [PubMed]

4.  Lee TX, Packer MD, Huang J, Akhmametyeva EM, Kulp SK, et al. (2009) Growth inhibitory and anti-tumour activities of OSU-03012, a novel PDK-1 inhibitor, on vestibular schwannoma and malignant schwannoma cells. Eur J Cancer 45:1709-1720

   [Crossref] [Google Scholar] [PubMed]

5. Escalante J, McQuade RM, Stojanovska V, Nurgali K (2017) Impact of chemotherapy on gastrointestinal functions and the enteric nervous system. Maturitas 105:23-29

   [Crossref] [Google Scholar] [PubMed]

6. Nanney III AD, El Tecle NE, El Ahmadieh TY, Daou MR, Ivan EN, et al. (2014) Intracranial aneurysms in previously irradiated fields: Literature review and case report. World Neurosurg. 81:511-519

   [Crossref] [Google Scholar] [PubMed]

7. Patil CG, Hayden M, Katznelson L, Chang SD (2009) Non-surgical management of hormone-secreting pituitary tumors. Clin Neurosci 16:985-993

   [Crossref] [Google Scholar] [PubMed]

8.  Ribatti D (2011) Novel angiogenesis inhibitors: Addressing the issue of redundancy in the angiogenic signaling pathway. Cancer Treat Rev 37:344-352

   [Crossref] [Google Scholar] [PubMed]

9. Bezjak A, Adam J, Barton R, Panzarella T, Laperriere N, et al. (2002) Symptom response after palliative radiotherapy for patients with brain metastases. Eur J Cancer 38:487-496

   [Crossref] [Google Scholar] [PubMed]

10. Fayette J, Soria JC, Armand JP (2005) Use of angiogenesis inhibitors in tumour treatment. 41:1109-1116

    [Crossref] [Google Scholar] [PubMed]