Bunker Shielding Design of Medical LINAC and Cobalt-60 Teletherapy Unit; Evaluation and Onsite Verification
Muhammad Isam Khan*, Rabia Khalil, Sara Niaz, Amna Bibi and Manahil Habib
Published Date: 2025-02-28Muhammad Isam Khan*, Rabia Khalil, Sara Niaz, Amna Bibi and Manahil Habib
Department of Medicine, University College of Medicine and Dentistry, Lahore, Pakistan
*Corresponding Author:
- Muhammad Isam Khan
Department of Medicine, University College of Medicine and Dentistry, Lahore, Pakistan
E-mail:isam.khan37@gmail.com
Received date: October 16, 2023, Manuscript No. IPIMP-23-18010; Editor assigned date: October 18, 2023, PreQC No. IPIMP-23-18010 (PQ); Reviewed date: November 01, 2023, QC No. IPIMP-23-18010; Revised date: January 12, 2025, Manuscript No. IPIMP-23-18010 (R); Published date: January 19, 2025, DOI: 10.36648/2574-285X.10.1.88
Citation: Khan MI, Khali R, Niaz R, Bibi A, Habib M (2024) Bunker Shielding Design of Medical LINAC and Cobalt-60 Teletherapy Unit; Evaluation and Onsite Verification. J Med Phys Appl Sci. Vol:10 No:1
Abstract
This study assessed the Linac and Cobalt-60 radiotherapy bunker designs, considering factors like wall thickness, composition, leakage radiation, and ventilation efficiency. It confirmed that the design met regulatory guidelines, offering effective radiation shielding and safety. These findings underscore the significance of adhering to such guidelines when designing and operating radiotherapy facilities, ensuring optimal radiation protection for patients, staff, and the public.
Keywords
Linac and Cobalt-60; Radiotherapy; Wall thickness; Composition; Leakage radiation; Ventilation efficiency
Introduction
Early in the 20th century, the potential dangers of radiation were recognized, and the International Commission on Radiological Protection (ICRP), one among the first agencies to establish standards, published the standard for radiation exposure. Radiation shielding is used to minimize and partially control the radiation exposure rate [1-3]. To safeguard the patients, staff, and general public who might be present in the passageways, rooms nearby, etc., radiation shielding is required. Lead, concrete, and steel are the materials utilized and for neutron shielding, borated polyethylene is used [4,5]. Radiation therapy using LINACs are rapidly increasing and being installed in various public and private cancer hospitals. As the latter produces high energy X-rays that ranges from 6 MV to 18 MV, It needs enough shielding to shield the personnel, patient's attendant, and general public from the damaging effects of radiation. At energies above 10 MV, protection against neutrons is also necessary. Controlled and uncontrolled zones have been set aside around the vault chamber [6].
To treat malignant tumors and other medical disorders, radiotherapy uses high-energy radiation beams. However, if they are not properly confined and managed, these radiation beams could be harmful to human health. The Cobalt-60 machine employs gamma rays released from radioactive Cobalt-60 to deliver radiation to the tumor, whereas the Linac machine delivers radiation to the tumor using high-energy electrons or photons. The Linac machine uses high energy electrons or photons to deliver radiation to the tumor, while the Cobalt-60 machine uses gamma rays emitted from radioactive Cobalt 60 to deliver radiation. The bunker design for these machines must consider the differences in the energy and type of radiation they produce [1].
Shielding calculations for radiotherapy bunkers are essential to achieve several goals
- Radiation protection: The primary purpose of shielding calculations is to protect individuals in and around the treatment facility from excessive radiation exposure. This includes patients undergoing treatment, medical staff, visitors, and the general public. Shielding materials such as concrete, lead, and steel are strategically placed to attenuate the radiation beams and reduce the radiation dose to acceptable levels.
- Compliance with regulations: Medical facilities that provide radiotherapy services are subject to follow regulatory requirements and guidelines that dictate the maximum allowable radiation exposure levels for different personnel categories. Shielding calculations help ensure that the facility's design and construction comply with these regulations, minimizing the risk of radiation-related health issues among staff and patients.
- Minimization of environmental impact: Proper shielding calculations prevent the leakage of radiation from the bunker into the environment. By containing radiation within the treatment area, these calculations contribute to minimizing the environmental impact of the facility and prevent unnecessary exposure of nearby populations.
- Long term facility viability: A well-designed bunker with appropriate shielding ensures the long term viability of the radiotherapy facility. It prevents structural damage and degradation caused by prolonged exposure to be ionizing radiation, minimizing the need for costly repairs or renovations.
- Risk management: Proper shielding calculations contribute to overall risk management in a radiotherapy facility. By identifying potential radiation exposure risks and addressing them through shielding design.
- Quality assurance: Shielding calculations are part of the quality assurance process for radiotherapy facilities. Ensuring that the shielding meets the required standards is a critical aspect of maintaining the facility’s credibility and reliability in delivering safe and effective treatments.
Two types of radiation have to be protected against: Primary radiation and secondary radiation i.e. leakage and scatter [3].
- Primary radiation-Primary beam: The beam that is emitted from the X-ray unit which passes through the window, aperture cone and other collimating device. Primary barriers are used to minimize primary radiation, and they include walls that the radiation is directly aimed at. Shielding of the side walls, floor, and ceiling constitutes the main radiation barrier. Compared to the secondary barrier, the primary radiation barrier will be significantly thicker.
- Secondary radiation-Secondary radiation: Also known as leakage radiation and scatter radiation, is the radiation produced if a primary beam interacts with materials (such as soft tissues, the human head, bones, etc.).
- Scatter radiation-Radiation: That is distributed around the treatment room and patient walls after being deflected from its intended course. In comparison to the radiation that was incident, the scattering contains less energy. The scattering radiation’s usage factor is taken to be one.
- Leakage radiation: The radiation that the machine’s treatment head produces and releases in every direction. When using LINAC, the leakage from the treatment head cannot be greater than 0.5%, and if the patient is present, the leakage has to be no greater than 0.1%.
Numerous research studies have been conducted on the topic of shielding calculations for radiotherapy bunkers. These studies aim to refine the understanding of shielding requirements, develop improved methodologies, and evaluate the effectiveness of different shielding materials and designs. The primary objective of performing shielding calculations for bunkers in radiotherapy is to create a safe and controlled environment where radiation treatments can be administered effectively while minimizing the risks associated with radiation exposure for patients, staff, and the general public.
The physical parameters that are used to quantify the radiation dose a patient receives during radiotherapy are known as dosimetric quantities. The principal dosimetric measurements utilized in radiotherapy include [1]:
- Absorbed dose: This represents the energy that a patient’s tissue absorbs per unit mass. It is measured in Gray (Gy) units.
- Equivalent dose: The equivalent dose quantifies the impact of radiation on biological tissue, considering fators such as the radiation type, energy, and the tissue’s sensitivity to radiation. It is expressed in units of Sievert (Sv).
- Effective dose: The effective dose is a comprehensive measure of the radiation dose received by the entire body, accounting for the varying sensitivities of different organs and tissues to radiation, measured in Sievert (Sv) [6].
- Work load: The volume and complexity of duties that radiation therapy specialists, including radiation therapists, radiation oncologists, and medical physicists, manage on a daily basis are referred to as a person’s “workload” in the context of radiation therapy.
- Occupancy factor: The occupancy factor is utilized to determine the effective dosage or equivalent dose that people who spend time in a certain region with radiation get.
- Use factor: The word “use factor” in radiation therapy refers to the percentage of time that a specific radiation source or piece of equipment is really being used or operating over the course of a given period [6].
Difference between LINAC and modern modalities
Linear Accelerator (LINAC)
Technology: LINAC, short for Linear Accelerator, is a traditional radiation therapy device that uses microwave technology to accelerate electrons and direct them into a target material, typically tungsten or other high-density metals, to produce high energy X-rays or photons for radiation therapy.
Treatment accuracy: LINAC treatments rely on external imaging techniques such as X-rays or CT scans to locate the tumor before each session. Patient positioning and tumor targeting can be affected by organ movement and changes in the patient's anatomy between sessions.
Treatment delivery: LINAC delivers radiation from various angles, typically 2-5, to converge on the tumor. This approach can result in radiation exposure to healthy surrounding tissues.
Treatment planning: Treatment planning is typically done using 3D conformal or Intensity-Modulated Radiation Therapy (IMRT) techniques.
Modern modalities (CyberKnife, TomoTherapy, MRLINAC)
CyberKnife
Technology: CyberKnife uses a robotic arm to deliver highly focused, high-energy X-rays (or photons) from many different angles with sub-millimeter accuracy.
Treatment accuracy: Real-time tracking and correction for organ motion during treatment ensure precise targeting, allowing for higher doses with minimal damage to surrounding tissue.
TomoTherapy
Technology: TomoTherapy combines a linear accelerator with a CT scanner, allowing for continuous delivery of radiation while imaging the patient. It uses Intensity-Modulated Radiation Therapy (IMRT) to shape the radiation dose.
Treatment accuracy: Daily CT scans enable adaptive treatment planning to account for anatomical changes, improving accuracy.
MR-LINAC
Technology: MR-LINAC integrates a linear accelerator with Magnetic Resonance Imaging (MRI) for real-time visualization during treatment. This enables continuous adaptation of the treatment plan.
Treatment accuracy: Real-time MRI guidance allows for tracking and adjusting for organ motion, enhancing accuracy and minimizing damage to healthy tissue.
Treatment delivery: CyberKnife, TomoTherapy, and MR-LINAC all offer more precise and adaptable treatment delivery compared to LINAC, reducing the risk of damage to healthy tissues.
Treatment planning: These modern modalities use advanced treatment planning techniques, such as image-guided and adaptive radiotherapy, to tailor radiation doses to the specific shape and location of the tumor.
Difference in shielding calculation
Shielding calculations for radiation therapy machines like LINAC, CyberKnife, TomoTherapy, and MR-LINAC involve assessing the amount of radiation protection needed to ensure the safety of patients, staff, and the public. Here are the key differences in their shielding calculations:
LINAC (Linear Accelerator)
X-ray shielding: LINAC machines primarily emit high-energy Xrays (photons). Shielding calculations for LINAC focus on attenuating these photons.
Collateral radiation: Shielding calculations also consider the production of secondary radiation, such as scattered photons and neutrons, which can contribute to the dose outside the treatment field.
CyberKnife
X-ray shielding: Like LINAC, CyberKnife uses X-rays (photons) for treatment. Shielding calculations for CyberKnife are like those for LINAC, but they may take into account the unique robotic arm and treatment delivery system.
Robotic arm considerations: The robotic arm's ability to deliver radiation from multiple angles necessitates thorough shielding calculations to ensure that all potential beam paths are adequately shielded.
All barriers (except ceiling) are primary barriers and there is no fixed isocenter.
TomoTherapy
X-ray shielding: TomoTherapy uses X-rays (photons) and a helical delivery technique. Shielding calculations must account for the continuous beam delivery and the potential for increased scatter.
CT imaging component: TomoTherapy machines incorporate a CT scanner. Shielding calculations need to consider the CT component's radiation output and leakage.
MR-LINAC (Magnetic Resonance Linear Accelerator)
Unique considerations: MR-LINAC combines a linear accelerator with an MRI machine. Shielding calculations for MRLINAC are complex and need to account for the unique magnetic and Radiofrequency (RF) fields associated with MRI, in addition to the X-ray radiation.
MRI shielding: MRI shielding is essential to contain the strong magnetic field and RF emissions. This typically involves ferromagnetic materials (e.g., steel) for the MRI room.
X-ray shielding: Shielding for the X-ray component follows similar principles as LINAC but requires special attention due to the coexistence of the MRI system.
Materials and Methods
In this research paper focused on radiation shielding, we examine the essential components of primary and secondary barriers and the methodologies for determining their thickness.
Primary barrier
The primary barrier is employed to shield against direct primary radiation and includes protective measures for the floor, ceiling, doors, and lateral walls. The thickness of the primary barrier is considerably greater than that of the secondary barrier. The transmission factor (B) for primary radiation is calculated using:
B=p(SAD)+d)2/WUT Equation 1
An alternative approach for determining primary barrier thickness involves calculating the number (n) of Tenth Value Layers (TVLs) via Equation 2:
n=log(1/B) Equation 2
Subsequently, the barrier thickness (t) can be determined based on the TVL of the energy beam in the shielding material using Equation 3:
t=n × TVL Equation 3
Secondary barrier
The secondary barrier is designed to protect against leakage radiation from the treatment head and scattered radiation from the patient and treatment room walls.
Leakage radiation from a LINAC should not exceed 0.5% in the absence of the patient and 0.1% when the patient is present. The required attenuation (BL) for shielding against leakage radiation is computed as per Equation 4:
BL=(1000 Pd2)/WT Equation 4
Like the primary barrier, an alternative method for determining barrier thickness is to calculate the number (n) of TVLs and then use Equation 3 for thickness determination.
Scatter radiation emanates from the patient and treatment room walls in all directions. Its intensity depends on various factors. The transmission factor (BS) required to reduce scatter radiation is determined by Equation 5:
Bs=(pd2 sec d2 sac)/(aWT(F/400)) Equation 5
Again, the alternative method of calculating barrier thickness is to compute the number (n) of TVLs and then use Equation 3 to find the thickness.
Maze calculations
When constructing a maze for radiation therapy, it is imperative to understand how X-rays and gamma rays interact with the patient and the surrounding walls. For X-ray machines operating at less than 10 MV and 60 Co sources, primary, leakage, and scattered radiation transmission factors are essential. For systems operating at or above 10 MV, neutron fluency also needs to be considered.
Total Dose at the Maze Entrance (Dd):
Dd =2.64(DpH +f x DwH+DLH+DTH) Equation 6
Where,
Dose arising from scatter by patient (DPH):
DpH=(WUα(F/400)α1 A1)/((dsca)(dsec)(d1))2 Equation 7
Dose arising from primary beam scattered by Wall (DwH):
DwH=WUHAH AR αH αR)/((dH dR dZ)2 Equation 8
Dose arising from transmission of primary beam through the maze wall (DwT):
DWT=WUHBpr APαP)/(dPd)2 Equation 9
Dose arising from head leakage scatter to the maze entrance (DLH):
DLH=LoWα1 A1/(di dM)2 Equation 10
Head leakage transmission to the maze entrance (DTH):
DTH=LoUWB/(dT)2 Equation 11
Gamma capture Dose (Dθ)
Capture gamma dose refers to the radiation dose produced when gamma rays are captured by certain materials. This dose contributes to the total radiation exposure in the maze and surrounding areas.
Dθ=(5.7 × 10-16 ) (θA) (10-d2/6.2) Equation 12
Where θA is the total neutron fluence, which is shown as:
θA=QN/(4π d21)+5.4 QN/(2πS+(1.26QN)/(2πS) Equation 13
Neutron Dose at maze Entrance (DE)
Neutron dose depends on gantry angle and room size. It is especially important when considering door calculations and is influenced by the total neutron fluence.
DE=W × DN
Where DN is calculated using the following formula:
DN=(2.4 × 10-15)(θA)(√(Ar/S1) (1.64)(10-d2/1.9)(10-d2/Tn) Equation 14
These calculations are fundamental for designing and evaluating the radiation shielding necessary to ensure the safety of personnel and the public in radiation therapy facilities.
Calculations of 15 MV LINAC
In this section, we determine the required thickness and width of the primary radiation barriers for wall A and wall B in a radiation therapy facility. The calculations are based on wellestablished equations and parameters to ensure radiation safety [7-9].
Primary barrier: For wall A, Primary radiation source (P) is 0.00002 Sv/wk (uncontrolled area), distance from point of interest to source origin (d) is 4.4 m, Workload (W) is calculated as 4000 Gy/wk, Use factor (U) is 0.25 (traditional value by NCRP 151) and Transmission factor (T) for unattendent parking lot is 0.0625 IAEA 47) [1].
Using Equation (1), the barrier transmission factor (Bp) is calculated as 2.33 × 10-6
Using Equation (2), we determine the number of Tenth Value Layers (TVLs) required as 5.63. The TVL for a 15 MV LINAC in concrete (primary beam) is 432 mm [1]. Therefore, the required thickness for the primary barrier is calculated as 7.8 ft.
For wall B, Primary radiation source (P) is 0.0002 Sv/wk (controlled area), distance from point of interest to source origin (d)=4.4 m, W=4000 Gy/wk, U=0.25 (traditional value by NCRP 151) [2], T=1 (treatment vault doors, IAEA 47) [1]. By similar method thickness of wall B is calculated as 8.1 ft.
Width of primary barrier (A and B)
Using the width of the barrier equation:
W=(0.4)(√2)d+0.6 Equation 15
With a distance (d) of 5.44 m, we calculate the required width as 11.8 ft.
Secondary barrier: For Wall A, the parameters used for primary barrier are same. Here, dsca=1 m, dsec=4.4 m, scattering coefficient (α) is 2.61 × 10-4 for 15 MV at an angle 90° [1], Field size at the patient (F)=1600 cm². The scatter radiation barrier is calculated using Equation 5 as 1.48 × 10-3. While thickness is calculated as 3.00 ft [10]. The transmission factor for leakage barrier is calculated from Equation 4 as 1.54 × 10-3 and thickness is calculated as 3.00 ft. The final thickness for wall A is 3.3 ft. Similarly, for Wall B, C, D, the thickness according to their parameters are found to be 3.57 ft, 3.93 ft, 3.8 ft.
Roof thickness: Barrier transmission factor for roof is calculated from Equation 1 and thickness is found to be 7.0 ft.
Where,
T=1 for controlled area
U=0.25
d=6.2
SAD=1 m
Maze calculation: The dose DPH at the maze entrance can be calculated by Equation 7 as
DPH=1.37 × 10-4
Where,
W=4000 Gy/wk
Up=0.25
α=1.05 × 10-3
F=1600 cm²
α1=2.03 × 10-2 (Reflection angle 0° for 0.5 MeV Photons, IAEA 47) [1]
A1=11.8 m²
dsca=1 m
dsec=8.4 m
d1=10.2 m
Dose arising from the primary beam scattered by the wall is calculated by Equation 8 which is DWH=1.6 × 10-5.
Where, αH=Wall reflection coefficient (Normal incidence and 75°reflection)=1.75 × 10-3 [1].
A1=8.82 m²
α1=Second reflection coefficient (Normal incidence and 75° reflections (0.5 MeV)=7.54 × 10-3 [1],
dH=2.8 m,
AH=2.82 m²
dr=5.6 m
dz=9.1 m
The dose arising from the head leakage to the maze entrance is found to be DLH=3.49 × 10-5 by using Equation 10.
Where, L0=Fraction of dose due to head leakage at 1 m=0.1%=1 × 10-3
α1=4.34 × 10-3 [1]
A1=11.8 m²
d1=7.7 m
dm=10.0 m
The dose of head leakage to the maze entrance can be calculated by Equation 11 and it is found to be 4.04 × 10-5.
Where,
B =1.99 × 10-3, dT=The total dose at the maze entrance Dd is Dd=5.7 × 10-4 by using Equation 6
Capture Gamma Dose (Dθ)
QN=3.2 × 1011 [1]
d1=8.4 m
d2=8.8 m
S=225 m2.
Using Equation13, we calculate θA=1.81 × 109 neutrons/m2.
Using Equation 12, we calculate Dθ=3.9 × 10-8 Sv/wk.
Weekly dose at maze door is calculated Using Equation 17, we calculate DC=1.5 × 10-4 Sv/wk.
Shielding thickness for lead is calculated Using Equation (3) with TVL for lead=6 [1], we find t=5 mm.
=1.26 x 10-7 Sv per x-ray Gy. Then, DE=(4000)(1.26 × 10-7)=5.04 × 10-4 Sv/wk.
Shielding thickness for Borated Polyethylene (BPE) is calculated using Equation (3) with TVL for BPE (45), we find t=32 mm [11].
Therefore, the required thickness of BPE for the maze entrance door to effectively reduce neutron and capture gamma dose to acceptable levels is determined to be 32 mm.
First we calculated the dose rate at iso centre=75 Gy.h-1, Dose rate at 1 m=48 × 106 μGy.h-1 and workload at isocentre=720 Gy/ week.
Weekly neutron Dose at maze Entrance (DE)
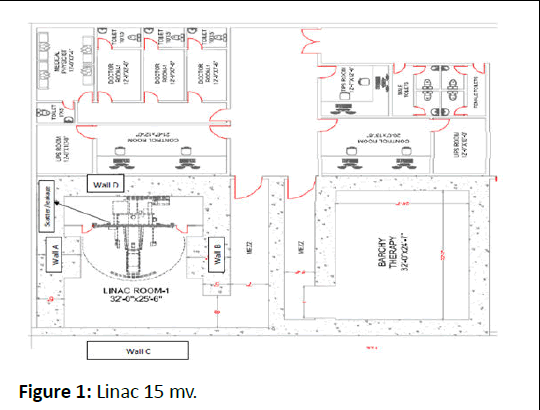
S1=7.8 m, where the remaining parameters remains the same. Using Equation 14, we calculate DN (Figure 1).
Figure 1: Linac 15 mv.
Cobalt-60 calculations
Primary barrier: The barrier transmission factor for primary barrier is calculated using IDR method. The formula is given as:
BIDR=(P)(SAD+d)2/(DRO) (T)] Equation 16
For wall A, P=0.00002 Sv/wk (uncontrolled areas), d=2.92 m, T=1/4 (corridor, IAEA-47) [1], DRO=48
10-6 μGy.h-1, SAD=0.8 m. using Equation 18, BIDR=8.649 × 10-6. Thickness is calculated using similar method as used in LINAC, which is found to be 3.6 ft, where the TVL of Cobalt-60 in concrete is 218 mm [1].
Wall B is calculated by similar method which is calculated as 3.59 ft.
Now, calculating IDR from Equation:
IDR=DR × B/(SAD+d)2 Equation17
IDR=32.84 μSv.h-1
Now, calculating TADR from Equation:
TADR=IDR × 3U/10 Equation 18
TADR=2.463 μSv.h-1
Width of Primary Barrier (A and B) is calculated using Equation,
Where d=2.92.
W=(0.3)(√2)d+0.6
W=6.03 ft
Secondary barrier: The required barrier transmission factor for scatter and leakage radiation at wall A, B and C can be determined by Equation (5) and (4). The thickness at Wall A is calculated as 2.41 ft and using Equation 17, IDR is calculated as 13.3 μSv.h-1. The thickness at Wall B is calculated as 3.08 ft and using Equation 17, IDR is calculated as 13.3 μSv.h-1. The thickness at Wall C is calculated as 2.4 ft and using Equation 17, IDR is calculated as 21.3 μSv.h-1 [12].
Roof thickness: The required barrier transmission factor for controlled area can be calculated by Equation (1) Where,
P=0.0002Sv/wk (controlled areas)
d=3.35 m
SAD=0.8 m
W=720 Gy/wk
U=0.25
T=1
The calculated transmission factor is 1.91 × 10-5. The required thickness is 3.3 ft. Whereas, the width is calculated using Equation 12 as 6.6 ft.
Maze calculation: The dose DPH at the maze entrance is calculated by Equation 7 as 1.16 × 10-4 Gy/week.
Where,
W=720 Gy/wk
Up=0.25
α=9.1 × 10-4
F=1600 cm2
α1=2.03 × 10-2
A1=6.0 m2
dsca=0.8 m
dsec=4.7 m
d1=5.3 m
Now, IDR can be calculated by using Equation 17 as 3.46 μSv.h-1
Dose arising from the primary beam scattered by the wall is calculated by Equation 8 as 1.62 × 10-5 Gy/wk.
Where,
αH=4.06 × 10-3
Ar=3.9 m2
αr=7.54 × 10-3
dH=2.0 m
AH=1.2 m²
dr=4.06 m
dz=4.9 m
Now, IDR can be calculated by Equation 17 as 1.08 μSv.h-1 +
W=720 Gy/wk,
Lo=0.1%=1 × 10-3
α1=1.07 × 10-2
A1=6 m2
di=4.1 m
dm=5.2 m
Where, the dose arising from the head leakage to the maze entrance is calculated by using Equation 10 as 1.016 × 10-4 Gy/wk. Now, IDR is calculated by using Equation 17 as 6.7 μSv.h-1
The dose of head leakage to the maze entrance can be calculated by Equation 11 as 3.15 × 10-5 Gy/wk.
Where,
B=4.0 × 10-3
Lo=1 × 10-3
dT=4.8 m
Now, IDR can be calculated by using Equation 17 as 2.08 μSv.h-1.
The total dose at the maze entrance Dd is calculated by Equation 6 as 6.6 × 10-4 Gy/week.
Now, IDR can be calculated by using Equation 17 as 13.32 μSv.h-1 (Figure 2).
Figure 2: Layout of Cobalt-60.
Results and Discussion
This research aimed to create effective radiation shielding for medical machines (C-Linac and Co-60) used in radiation therapy. Through scientific methods, we determined shielding thickness for walls, doors, and mazes to ensure safety for medical staff, patients, and the public. Collaboration with experts led to compliant and tailored designs following regulations and standards (Table 1). Our detailed research enhances radiation protection knowledge in healthcare, promoting safety for professionals and patients in radiation therapy [13,14].
| Parameter name | Energy | Needed values (from calculation in ft) |
Our designed values | ||||||
| Wall A | Wall B | Wall C | Wall D | Wall A | Wall B | Wall C | Wall D | ||
| For primary barrier | 15 MV LINAC | 7.8 | 8.1 | - | - | 8.2 | 8.2 | - | - |
| Cobalt-60 | 3.6 | 3.6 | - | - | |||||
| For secondary Barrier | 15 MV LINAC | 3.4 | 3.4 | 3.9 | 3.8 | 4 | 4 | 4.5 | 4.5 |
| Cobalt-60 | 3 | 2.7 | 2 | - | 3.5 | 3.5 | 2.5 | - | |
Table 1: Theoretical and designed thickness values of bunker of 15 MV and Cobalt 60.
Conclusion
In conclusion, this reasearch successfully contributed in designing effective radiation shielding for C-Linac and Co-60 machines in radiation therapy. Collaboration with experts, mathematical techniques, and adherence to guidelines led to comprehensive and practical shielding designs. This enhances safety for healthcare workers and patients, underscoring the significance of radiation protection in healthcare settings.
References
- International atomic energy agency (2006) Radiation protection in the design of radiotherapy facilities. Safety Reports Series, IAEA, Vienna.
- Beyzadeoglu M, Ozyigit G, Ebruli C (2010) Basic radiation oncology. 1st Edition, Springer Berlin, Heidelberg, 575
- Khan F, John P (2014) Gibbons-The physics of radiation therapy. 5th Edition. Wolters Kluwer Health. 624
- Amestoy W (2015) Review of medical dosimetry. Springer, Heidelberg, New York.
- Ervin B (2016) Radiation physics for medical physicists. Springer Nature.
- Morrow A (2019) Radiation shielding and bunker design. St. Vincets’s private hospital, Elm Park, Trinity College of Dublin.
- Cedric TM, Odette SN, Fotue AJ (2020) The structural shielding of the new radiotherapy bunker at the general hospital of Yaounde in Cameroon: An enhancement of radiation protection. Dual Diagn Open Acc 5:13
- Johns HE, Cunningham JR (1983) The physics of radiology. Thomas Publisher.
- Al-Senan RM, Al-Dweri FM, Marashdeh MW (2021) Evaluation of radiation leakage from radiotherapy machines at different beam energies and field sizes. Pract Radiat Oncol 1-9
- Nisbet A, Beaven EA, Thwaites DI (2003) Measurement of the leakage and scatter radiation from a radiotherapy linear accelerator: A comparison of experiment and theory. Phys Med Biol 48:2517
- Turner JE (2008) Atoms, radiation, and radiation protection. John Wiley and Sons.
- Das IJ, Cheng CW, Chopra KL (2016) Radiation shielding and radiographic imaging. CRC Press.
- Goitein M (2007) Radiation oncology: A physicist's-eye view. Springer Science and Business Media.
- Kha MR, Aljarrah KM, Muhammad S (2017) Shielding, filtering, and transforming the radiation safety and radiation shielding. Lambert Academic Publishing.
Open Access Journals
- Aquaculture & Veterinary Science
- Chemistry & Chemical Sciences
- Clinical Sciences
- Engineering
- General Science
- Genetics & Molecular Biology
- Health Care & Nursing
- Immunology & Microbiology
- Materials Science
- Mathematics & Physics
- Medical Sciences
- Neurology & Psychiatry
- Oncology & Cancer Science
- Pharmaceutical Sciences