Journal of Medical Physics and Applied Sciences

Keywords

Hawking radiation; Kerr-Newman black hole; Damour-Runi method; Quantum theory

Introduction

Hawking established theoretically in 1975 that black holes can emit thermal radiation and that the temperature associated with it is correct. The thermal radiation of a black hole has become a hot topic in theoretical physics in recent years [1,2]. Many useful methods, like the tunneling approach, the Hamilton Jacobi method, and the gravitational anomaly method, attempt to explain the dynamical genesis of black hole thermal radiation. Following that, with black hole evaporation, there is a paradox of information loss, which means that the pure quantum state will be disintegrated into the mixture. In Quantum Field Theory, the ingoing state is the pure state, but the outgoing state is the mixture, so the underlying unitary theory is violated. In addition, Hawking believed that the black hole's thermal radiation is due to the quantum tunneling effect, which is triggered by a vacuum caution near the event horizon, causinga pair of particles to form just inside the horizon, with the positive energy particle tunneling out and the negative anti-particle being absorbed by the black hole. In other words, we can consider that the particles created just outside the horizon, the negative energy anti-particle is tunneled into the horizon because the negative energy orbit only exists within the horizon, and the positive energy particle is left outside the horizon and moves towards the infinite distance, forming the Hawking thermal spectrum. Because both narrative forms involve tunneling, the tunneling barrier must be identified to accurately depict the tunneling process and obtain the correct radiation spectrum. In 1976 [3], Damour and Runiused relativity rather than the second quantilization. To validate the Hawking radiation from black holes, Quantum Mechanics in Curved Space-Time was used. They argued that a massive charged particle may tunnel out over the horizon using a wave function, resulting in the formation of a pair: one particle would move out, while the other would fall back towards the singularity. They were able to obtain the spectrum of Hawking radiation in this manner.

Kraus and Wilczek [4] developed a semi-classical method to describe Hawking radiation as a tunnelling process in which a particle moves in dynamic geometry, and Parikh and Wilczek [5] and Vagenas [6] carried out research on the tunneling radiation characteristics of static spherically symmetric Schwarzchild black hole and Reissner-Nordstr om black hole. The results show that, when energy conservation and the un_xed space-time background are taken into account, the resultant radiation spectrum is not strictly thermal, which is a correct modification to the Hawking radiation spectrum. The method overcomes Hawking radiation flaws, pointing out that self-gravitation among particles provides the tunneling barrier. Finding a wellbehaved coordinate system near the event horizon to determine the emission rate is a fundamental insight. Tunneling not only provides a valuable technique for verifying black hole thermodynamic parameters, but it also provides an alternative conceptual means of comprehending the underlying physical process of black hole radiation. Hawking radiation from Anti-de Sitter black holes was researched by Hemming and Keski-Vakkuri (2001), and Medved [7] explored those from a de Sitter cosmic horizon. It has been successfully applied to a large variety of exotic space-times [8-13], demonstrating its robustness. However, determining the imaginary part of the action for the exiting particle is a difficult task. However, they are all limited to spherically symmetric black holes. The Hawking radiation from a static spherically symmetric black hole was calculated using the Damour-Runi method and factoring the self-gravitation interaction and energy conservation [14]. Their findings reveal that the radiation isn't precisely thermal, and that this nonthermal Hawking radiation can transport data from the black hole. This can be used to explain the black hole information

paradox, and the process also meets unitary requirements. Han and Hao investigated the Kerr black hole's non-thermal Hawking radiation [15]. We seek to extend this method to the stationary axi-symmetry Kerr-Newman black hole in this study, obtaining the Hawking spectrum in a dragging coordinate system as well as tunneling rates at the event and cosmological horizon. The corrected non-thermal Hawking radiation of the stationary axisymmetry black hole is calculated using a new method that is more precise and general. In Section 2, we look at the Damour- Runi approach for calculating the accurate thermal spectrum in a dragging coordinate system. In Section 3, we examine analytical continuations and the self-gravitation interaction to look into the black hole's tunneling radiation properties. Section 4 ends with a discussion and a conclusion.

Review of the Damour-Ruffini Method

We consider the Kerr-Newman metric of the form

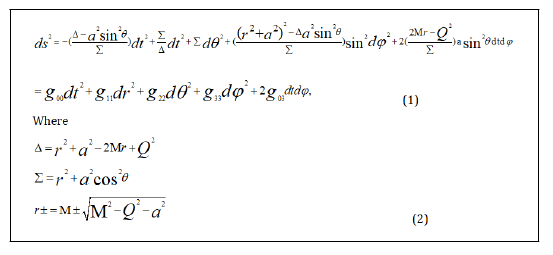
Here M denotes the black hole's total mass, a denotes the black hole's angular momentum per unit mass, and Q denotes the black hole's charge. The event horizon's surface gravity is

At the radius of the event horizon, the metric (1) has a coordinate singularity. To apply Damour-Ruffini's work to Kerr space-time, we must _rst identify a coordinate system that will perform well at the event horizon and whose coordinate clock synchronization can be transmitted from one location to another.

First, we examine the dragging coordinate system. Let

The space-time metric for the Kerr-Newman black hole can be expressed as

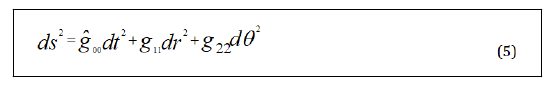
In four-dimensional Kerr-Newman space-time, the line element (5) represents a three-dimensional hyper-surface. Using the Damour-Ru_ni approach, we may obtain the Hawking radiation's pure thermal spectrum. This means that in the dragging coordinate system, we may also consider non-thermal Hawking radiation, where

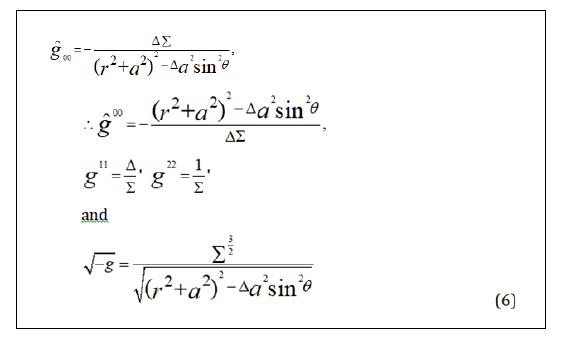
The Klein-Gordon equation in curved space-time is

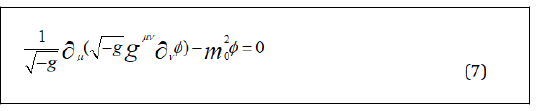
With equation (5), the Klein-Gordon equation can be reduced

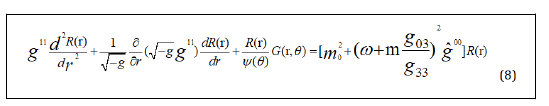
where

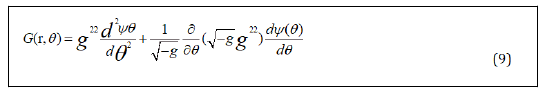
and φ,the wave function has been separated as

Introducing the Tortoise coordinates

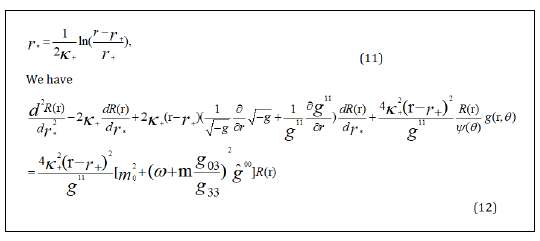
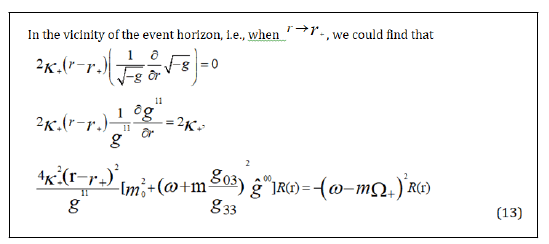
Thus, we can write equation (12) near the event horizon, in the standard wave equation as:

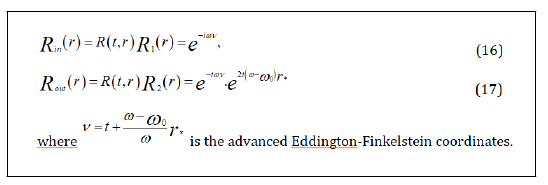
The Self-Gravitation Interaction and Analytical Continuations

Near the event horizon, R_out can be written as

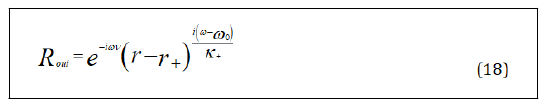
The Rout has a logarithmic singularity and it is not analytic on the event horizon r₊. By analytical continuation rotating -π through the lower-half complex r-plane, we have

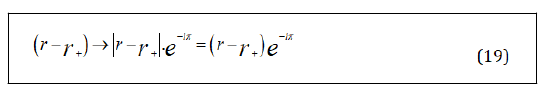
Then near the event horizon r₊, Rout can be rewritten as

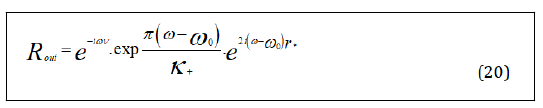
The scattering probability of the outgoing wave at the event horizon is

We can now assume that the emitting particles have a spacetime back-reaction. When a particle with energy ω_i, charge e_i, and angular momentum ji emerges from a black hole, M

For many particles, assuming that they radiate one by one, we have

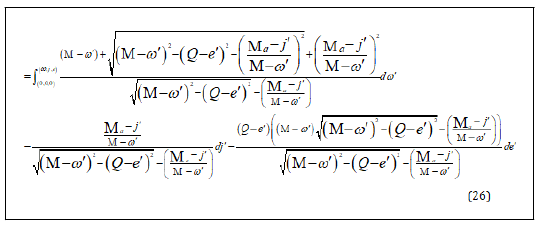
We don't have to do the integration directly to make the calculation easier. Instead, we take the following approach: making use of the entropy S of the black hole, satisfying the first law of thermodynamics, we have

Where A is the area of the black hole horizon, and we can easily obtain that

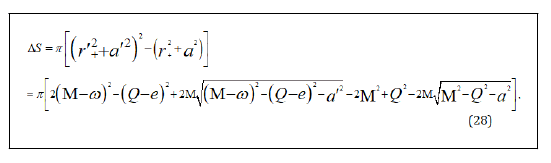
Where ΔS is the entropy change of the black hole between before and after the emission. Then we have

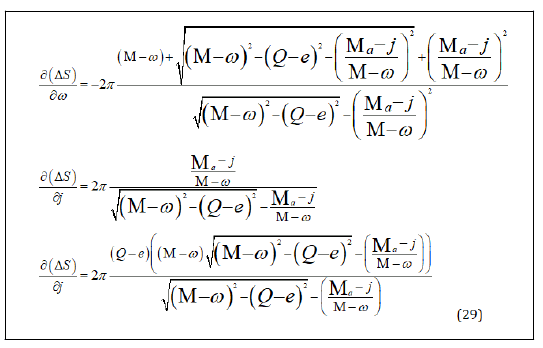
Comparing eq. (26) with eq. (29), we find that the integration in Eq. (26) satis_es the total differential condition. So Eq. (26) can be calculated out as following:

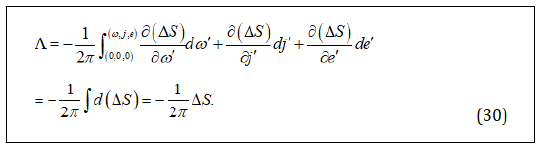
So the emission rate is given by

The underlying unitary theory is clearly present in this conclusion. In reality, quantum theory demonstrates that the outgoing-wave transmission can be written as

Where aif is the amplitude for the tunnelling action, and 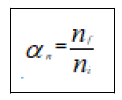is a phase factor with ni and nf being the sum of the number of beginning and end states, respectively. The phase factor is calculated by adding all final states together and averaging all initial states. The number of _nal states, on the other hand, is simply expressed in exponential form by the final states entropy, whereas the number of initial states is expressed in exponential form by the initial states entropy. We obtain which is in agreement with our result Eq. (31). Is as same as Eq. (33).

Conclusion

In this study, we show that taking into consideration the selfgravitational interaction of the radiant particle energy with the space-time background, the permeation ratio of the outgoing wave revises the thermal radiation spectrum from the Kerr- Newman black hole. This deduced result is in contrast to the earlier tunnelling-based study of the same subject, and it satis_es the unitary. However, we utilize a different approach that is more straightforward, direct, and tactile in nature. Furthermore, the computation is straightforward, and we don't need to worry about whether a radiant particle has a rest mass. When considering the self-gravitational interaction, it is clear that the outgoing-wave transmission ratio in the event area appears to depart from the black hole's thermal radiation spectrum, which may carry related information about the material that makes up the black hole. This finding could lead to a solution to the problem of information loss. In fact, if we use the Damour-Rffini method to calculate the Hawking radiation of the Kerr-Newman black hole without taking into account the self-gravitational interaction of the radiation energy with the time-space background, we get a precise radiation spectrum of the tunnelling process through the event area. In Eq. (12), the outgoing wave possesses a potential barrier between the event area and infinite distance. As a result, the black hole radiation spectrum, dispersed by the shape, appears gray to an observer staring at the event area from an infinite distance.

References

1. Hawking SW (1974) Black hole explosions. Nature 248: 30.

   [Crossref] [Google Scholar]

2. Hawking SW (1975) Particle creation by black holes. Commun Math Phys 43: 199.

   [Crossref] [Google Scholar]

3. Damuor T,  Ruffini R (1976)  Black hole evaporation in the klein-sauter-heisenberg-euler formulation. Phys Rev D 14: 332.

   [Crossref] [Google Scholar]

4.  Kraus P, Wilczek F (1995) Self-interaction correction to black hole radiance. Nucl Phys B 433: 403-420.

   [Crossref] [Google Scholar]

5.  Parikh MK, Wiclzek F (2000) Hawking radiation as tunneling. Phys Rev Lett 85: 5042.

   [Crossref] [Google Scholar] [Indexed]

6.  Venegas EC (2001) Are extremal 2d black holes really frozen? Phys Lett B 503: 399-403.

   [Crossref] [Google Scholar]

7.  Medved AJM (2002) Radiation via tunneling from a de sitter cosmological horizon. Phys Rev D 66:124009.

   [Crossref] [Google Scholar]

8. Parikh MK (2004) A secret tunnel through the horizon. Int J Mod Phys D13: 2351-2354.

   [Crossref] [Google Scholar]

9.  Zhang J, Zhao Y, Mod Z(2005) Hawking radiation via tunneling from kerr black holes. Phys Lett A 20: 1673-1681.

   [Crossref] [Google Scholar]

10.  Setare MR, Vagenas EC (2005) Self-gravitational corrections to the cardy–verlinde formula and the frw brane cosmology in sds5 bulk. Int J Mod Phys A 20:7219-7232.

    [Cross ref] [Google Scholar]

11.  Liu WB (2006)  New coordinates for btz black hole and hawking radiation via tunneling. Phys Lett B 634: 541.

    [Crossref] [Google Scholar]

12. Zhang JY, Fan JH (2007)  Tunnelling effect of charged and magnetized particles from the kerr–newman–kasuya black hole. Phys Lett B 648:133-138.

    [Crossref] [Google Scholar]

13.  LIU WB (2007) Damour-ruffini method and nonthermal hawking radiation from reissner-nordstrom black hole. Acta Phys Sin 56: 6164.

    [Crossref] [Google Scholar]

14.  Kerr RP (1963) Gravitational field of a spinning mass as an example of algebraically special metrics. Pyhs Rev Lett 11: 237.

    [Crossref] [Google Scholar]

15. Agheben M, Nadalini M, Vanzo L Zerbini S (2005) Hawking radiation as tunneling for external and rotating black holes. J High Energy Phys 14:505.

    [Crossref] [Google Scholar]